Change of Base Formula

Change of Base Calculator

The Change of Base Formula: A Simple Guide

Imagine you’re trying to solve a puzzle: “How many times do I multiply 5 by itself to get 100?”

This is essentially asking for log base 5 of 100. But here’s the catch: most calculators only have buttons for log base 10 ( $\log$ ) or natural log ( $\ln$ ). So how do you solve this?

Enter the Change of Base Formula

This handy trick lets you rewrite a logarithm with any base into a fraction using bases your calculator understands (like 10 or $e$ ). Here’s the formula:

\log_b(a) = \frac{\log_c(a)}{\log_c(b)}

Translation: To find $\log_b(a)$ , divide the log of $a$ (using any base $c$ ) by the log of $b$ (using the same base $c$ ).

Why does this work?

Let’s break it down:

Suppose 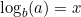$\log_b(a) = x$ . By definition, $b^x = a$ .
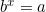Take the log of both sides with a base you know (like base 10):

$\log_{10}(b^x) = \log_{10}(a)$

Use the logarithm power rule ( $\log_b(a^n) = n \cdot \log_b(a)$ ):

$x \cdot \log_{10}(b) = \log_{10}(a)$

Solve for $x$ :

$x = \frac{\log_{10}(a)}{\log_{10}(b)}$

Voilà! The formula converts $\log_b(a)$ into a ratio of logs you can compute.

Examples to Try

Calculate $\log_5(100)$ :
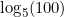– Using base 10: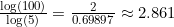 $\frac{\log(100)}{\log(5)} = \frac{2}{0.69897} \approx 2.861$ .
– Check: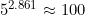 $5^{2.861} \approx 100$ .
Find $\log_2(16)$ :
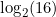– Using natural logs: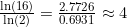 $\frac{\ln(16)}{\ln(2)} = \frac{2.7726}{0.6931} \approx 4$ .
– Check: $2^4 = 16$ .

Why It’s Useful

Accessibility: Compute logs with any base, not just 10 or $e$ .
Flexibility: Choose base 10 or $e$ —whichever is easier.
Applications: Used in computer science, finance, and engineering for problems involving exponential growth or decay.

Remember: The numerator and denominator must use the same base. And avoid bases ≤0 or 1—they don’t work for logs!

In short, the change of base formula is your calculator’s best friend, turning tricky log problems into simple division. Next time you’re stuck, just “change the base” and crunch the numbers!